[AI] 인공지능 이해를 위해 필요한 수학 지식들

인공지능을 공부하다보면 많은 수학적 지식이 필요하다. 그 중에서 행렬 분해, 블록 최적화, 주성분 분석에 대해 자세히 알아본다.

1. 행렬 분해(Matric Decomposition)

인공지능의 데이터는 주로 행렬로 표현되는데 이를 이해하기 위해 행렬과 관련된 수학적 지식에 대해 알아보자.

1-1. determinant(행렬식)

determinant는 어느 행렬의 역행렬 존재 여부를 판단할 수 있는 중요한 값이다. 2x2 행렬의 determinant는 아래와 같이 구할 수 있다.

\[A =\begin{pmatrix} a & b \\ c & d \end{pmatrix} \\ det(A) = ad - bc\]

식 \(det(A) = \sum_{k=1}^n (-1)^{k+j} a_{kj} det(A_{k,j})\)

이렇게 구한 determinant의 값이 0이면 해당 행렬의 역행렬이 존재하지 않는다.

역행렬(inverse matrix)?
주어진 행렬과 곱했을 때, 단위 행렬을 생성하는 행렬을 의미한다. 역행렬은 기호로 $A^{-1}$로 표현한다.
$$ A \cdot A^{-1} = A^{-1} \cdot A = I

determinant는 아래와 같은 유용한 성질들을 가진다.

• 곱셈에 대한 성질 : $ det(AB) = det(A) \cdot det(B) $
• 전치 행렬에 대한 성질 : $ det(A^T) = det(A) $
• 역행렬에 대한 성질 : $ det(A^{-1}) = \frac{1}{det(A)} $
• 삼각 행렬에 대한 성질 : $ det(T) = \prod_{i=1}^n T_{ii} $
• 스칼라 곱에 대한 성질 : $ det(kA) = k^n \cdot det(A) $

1-2. Trace(대각합)

대각합 정사각 행렬의 대각선 원소(diagonal entry)들의 합으로 정의된다.

\[tr(A) = \sum_{i=1}^n a_{ii}\]

그리고 대각합 아래와 같은 성질을 지닌다.

• 합에 대한 성질 : $ tr(A+B) = tr(A) + tr(B) $
• 스칼라 곱에 대한 성질 : $ tr(\alpha A) = \alpha tr(A) $
• 단위행렬에 대한 성징 : $ tr(I_n) = n $

2. EigenVector(고유 벡터)

nxn 행렬 A가 있을 때, 행렬 A의 고유값(eigenvalue)을 $\lambda$, 고유벡터(eigenvector)를 $x$라 하면 아래와 같은 관계를 가진다.

\[Ax = \lambda x\]

고유 벡터는 행렬 A에 의해 변환될 때 크기는 변하지만 방향이 변하지 않는 벡터로, 위의 식은 행렬 $Ax$ 는 고유 벡터 $x$를 방향은 유지하되, 크기를 $\lambda$ 배 만큼 확대하거나 축소한 것임을 의미한다.

고유 벡터를 구하기 위해서는 $(A-\lambda I)x = 0$을 풀면 고유값 $\lambda$에 대응하는 고유 벡터 $x$를 구할 수 있다. 그리고 저 식이 존재하기 위해서는 $(A-\lambda I)$가 비가역 행렬이어야 한다. 즉, $det(A-\lambda I) = 0$이어야 한다.

흥미로운 점은, 이렇게 구한 고유값 $\lambda$은 행렬 A의 determinant와 대각합과 관계가 있다.

\[det(A) = \prod_{i=1}^n \lambda_i \\ tr(A) = \sum_{i=1}^n \lambda_i\]

2-1. Cholesky Decomposition

Cholesky Decomposition은 주어진 대칭 행렬을 작은 행렬의 곱으로 분해하는 것을 말한다. 만약 행렬 A가 대칭이고 모든 고유값이 양수일 때, 행렬 A는 아래와 같이 표현이 가능하다. $L$은 lower triangular matrix를 의미하며, 행렬 A의 Cholesky factor라고 부른다.

\[A = LL^T\]

이를 활용하면 행렬 A의 determinant를 쉽게 계산할 수 있다.

\[\begin{align*} &det(A) = det(L)det(L^T) = det(L)^2 \\ &det(L) = \prod _i l_{ii} \end{align*}\]

2-2. Eigen Decomposition

주대각선 외의 모든 원소가 0인 행렬을 대각 행렬(Diagonal Matrix)이라고 하며, 대각 행렬의 경우에는 지수승, 역행렬, determinant 계산이 간편한다. 이러한 성질을 사용하기 위해 일반 행렬을 대각 행렬을 사용해서 표현할 수는 없을까?

정방 행렬 A를 다음과 같이 대각 행렬을 사용해 표현 가능한 경우를 diagonalizable 하다고 하며, P는 A의 고유벡터를 열벡터로 가지는 행렬이고, D는 A의 고유값들을 대각으로 가지는 대각 행렬을 의미한다.

\[A = PDP^{-1}\]

위의 식을 활용하면 지수승, 역행렬, determinant 계산이 편리하다.

\[\begin{align*} &A^k = PD^kP^{-1} \\ &A^{-1} = PD^{-1}P^{-1} \\ &det(A) = det(P)det(D)det(P^{-1}) = det(D) = \prod _i d_{ii} \end{align*}\]

만약 A가 대칭 행렬인 경우에는 직교 대각화가 가능한데, 이를 Eigen Decomposition(또는 EigenValue Decomposition, EVD)라고 한다. 행렬 Q는 A의 고유벡터들로 이루어지며, 고유벡터는 서로 직교한다.

\[A = QDQ^{-1}\]

2-3. Singular Value Decomposition

만약 대칭이 아니고 정방 행렬이 아닌 A에 대해서 분해를 하고 싶을 때는 Singular Value Decomposition을 수행해야 한다. 행렬 A가 mxn 크기의 행렬일 때, 행렬 U는 mxm크기의 직교 행렬, $\sum$은 mxn 크기의 대각행렬, 행렬 $V^T$는 nxn 크기의 직교 행렬이다.

\[A = U \sum V^T\]

$\sum$의 diagonal entries를 singular values라고 하며, U와 V의 각 벡터들을 left, tight singular vectors라고 한다.

3. Convex Optimization

기계학습에서 최적화 단계는 모델의 좋은 파라미터를 찾는 과정으로 매우 중요하다. 최적화 문제는 크게 unconstrained 최적화, constrained 최적화, convex 최적화 문제로 나눌 수 있다.

3-1. Unconstrained 최적화

어떠한 함수가 있을 때, 그 함수를 최적화하는 지점을 찾을 때, gradient 정보(미분이 0이 되는 지점)를 이용했다.

uncontrained, 즉, 제약이 없는 최적화 문제는 주로 gradient 알고리즘을 사용해서 해결한다. gradient 알고리즘은 주로 재귀적으로 다음과 같이 표현할 수 있다.

\[x_{k+1} = x_k + \gamma_{k}d_k\;\;(x_0은\;random)\]

방향 d가 함수 $f(x)$의 gradient와 내적값이 0이 될 때, 해당 방향으로 적절한 step size $\gamma$만큼 이동하면 이전보다 더 낮은 지점을 향해 다가갈 수 있다. 그리고 함수 f(x)는 주로 데이터의 손실함수로 정의가 된다.

3-2. Constrained 최적화

하지만 x에 대해 특정한 제약 조건(constrained)이 있다면, gradient 알고리즘을 바로 적용하기엔 무리가 있다.

보통 제약 조건은 다음과 같이 정의된다.

• $g_i(x) \le 0$ 일 때, $f(x)$를 최소화하라.
• $h_j(x) = 0$ 일 때, $f(x)$를 최소화하라.

이러한 문제들을 라그랑주 듀얼 함수(Lagrange Dual Function) 사용해 해결할 수 있다.

\[L(x, \lambda, v) = f(x) + \sum_{i=1}^m \lambda_ig_i(x) + \sum_{i=1}^p v_i h_i(x)\;\; (\lambda \ge 0)\]

이때, $\lambda$ 또는 $v$를 Langrange multiplier 혹은 dual variable이라 한다. 그리고 아래의 함수를 라그랑주 듀얼 함수하고 한다.

\[D(\lambda, v) = inf_x L(x, \lambda, v)\]

듀얼 함수로 구한 값은 항상 최적화보다 작거나 같다. 따라서 우리는 듀얼함수의 값을 최적화 값의 하한선으로 생각할 수 있다. 이러한 성질을 약한 이중성(Weak Duality)이라고 한다.

듀얼함수의 최적화는 항상 풀 수 있기 때문에 이를 최대화하여, 최적값에 최대한 가깝게 구하도록 한다.

3-3. Convex 최적화

convex 최적화 문제를 다루기 위해선 우선 convex 집합과 convex 함수 개념에 대해 이해할 필요가 있다.

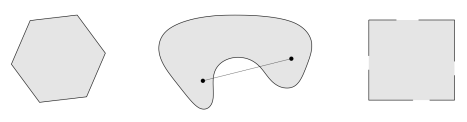
convex 집합은 집합 내의 두 점을 이은 선분 위의 모든 점이 해당 집합 내에 모두 포함되는 집합을 의미한다.

즉, 집합 C의 어떠한 두 점 $x1$, $x2$을 잇는 $\theta x1 + (1-\theta) x2$의 모든 점이 집합 C에 포함된다면 집합 C를 convex set이라고 한다.

위의 그림에서 제일 왼쪽 그림은 convex set이고 나머지 두 그림은 convex set이 아니다.

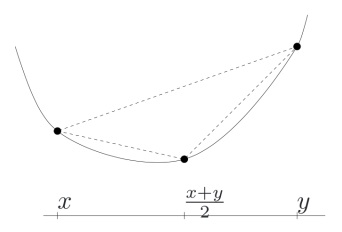
convex 함수(볼록 함수)는 그래프가 아래쪽으로 복록한 형태를 갖는 함수를 말한다

함수 $f(x)$가 convex 함수가 되기 위해서는 함수 내의 두 점을 이은 직선이 함수 그래프 위에 존재해야 한다.

\[f(\theta x1 + (1-\theta) x2) \le \theta f(x1) + (1-\theta) f(x2)\]

convex 함수인지 확인하기 위해서는 두 가지 방법이 있다.

• First-order condition

  f가 미분 가능 할 때, 접선보다 함수가 위에 있다.

  \[f(y) - f(x) >= \nabla f(x)^T(y-x)\]

  만약 $\nabla f(X) = 0$ 즉, $f(y) \ge f(x)$인 지점이 최솟값이다.

• Second-order condition

  이차 도함수(해시안 행렬)가 양수이거나 양의 준정부호(Positive Semi-definite)이어야 한다.

convex 함수는 지역 최적해가 글로벌 최적 해와 동일하며, convex 최적화는 목적함수와 제약 조건이 모두 convex 함수로 구성될 때 최적화를 구하는 문제이다.

이전에 constrained 최적화에서는 $d^* \le p^$인 약한 이중성이 성립되었다. 하지만 convex 최적화에서는 $d^ = p^*$ (strong duality)를 만족하기에 풀기 쉽다.

3-4. KKT (Karush-Kuhn-Tucker) 조건

KKT 조건은 최적화 문제에서 유효한 해를 찾기 위한 필요 조건을 제공한다.

특히 convex 최적화에서는 KKT 조건이 필요충분 조건이 된다.

먼저 라그랑주 함수를 아래와 같이 정의하고 라그랑주 함수에 대해 기울기가 0인 지점을 찾는다.

\[\begin{align*} &L(x, \lambda, v) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^p v_j h_j(x) \\ &\nabla_x L(x, \lambda, v) = 0 \end{align*}\]

기울기가 0인 지점의 x 값 중 아래 조건을 만족하는 경우에 최적해가 된다.

1. 기존의 제약 조건 만족

   $ g_i(x) \le 0 \ h_j(x) = 0 $

2. 듀얼 변수 조건 만족 - 라그랑주 승수가 양수여야 한다.

   $ \lambda_i \ge 0 $

3. 상호 보완성 조건 만족 - 활성화된 제약에서 라그랑주 승수가 0이 아니고, 비활성된 제약에서는 라그랑주 승수가 0이어야 한다.

   $ \lambda_i g_i(x) = 0 $

참고

본 포스팅은 LG Aimers 강좌 중 카이스트 신진우 교수님의 ‘Mathematics for ML’에서 학습한 내용을 정리한다.