[AI] 지도 학습1

1. 지도학습

지도 학습은 컴퓨터에게 문제와 정답 쌍을 제공하는 형태로 학습하는 방법을 말한다. 지도 학습의 예로는 아래와 같은 것들이 있다.

• Image Classification : 이미지의 카테고리를 맞히는 문제
• Text Classification : 주어진 문장이 긍정적인지 부정적인지 파악하는 문제
• Next Word Prediction : 주어진 글에 이어질 단어를 예측하는 문제
• Translation : 주어진 문장을 다른 언어로 번역하는 문제
• Price Prediction : 이전 10일치의 가격을 보고 다음날 주식 가격을 예측하는 문제

지도학습의 종류는 크게 분류와 회귀로 나눠진다. 분류는 고를 수 있는 정답이 정해져있어 주어진 입력에 대해 속하는 정답을 선택하는 문제이고, 회귀는 연속적인 수치 데이터를 예측하는 문제이다. 먼저 회귀 문제에 대해 자세히 알아본다.

2. 회귀(Regression)

먼저 모든 데이터를 완벽히 표현하는 정답 함수를 f이라고 하자. 그러면 우리는 이러한 f에 최대한 근접한 함수 g를 구하는 것이 목표이다. 이때, 함수 g에 대해 너무 큰 자유도가 주어지면 문제 해결이 어려울 수 있으므로 함수 후보군(=함수 클래스)인 G를 미리 정의한다. 즉, G 함수 중에서 가장 f*에 근접한 함수 g를 찾는 목표로 축소시키는 것이다.

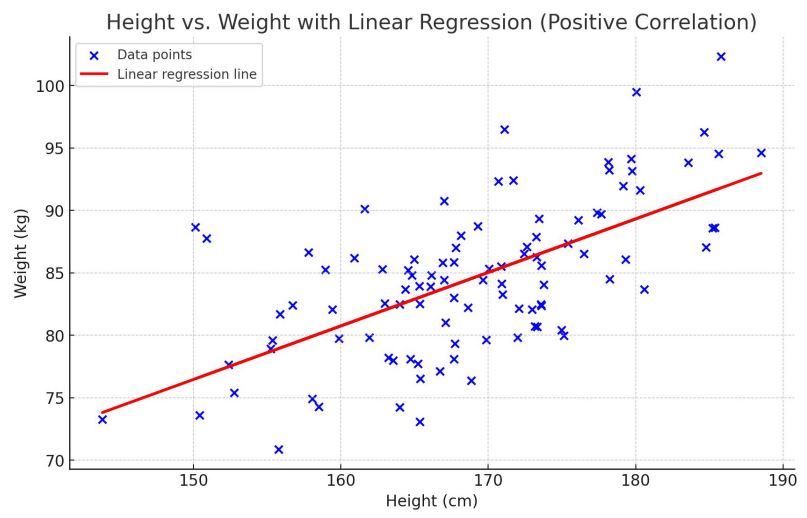
예를 들어, 주어진 키를 바탕으로 몸무게를 예측하는 모델을 개발하고자 한다. 데이터를 완벽히 표현하는 정답 함수 f*의 형태를 모르지만 일단 우리는 선형 함수 중에서 g를 찾고자 한다. 그러면 함수 클래스 G는 선형 함수로 정의된다.

• $G = g_{a,b}(x) = g_{\theta}(x) = ax+b $ (x는 입력, $\theta = (a,b)$)

2-1. 손실함수

하지만 위 이미지에서 보다시피 선형 함수로는 모든 데이터를 완벽히 표현할 수 없다. 그러면 선형 함수와 f*의 근사도는 어떻게 측정할 수 있을까?

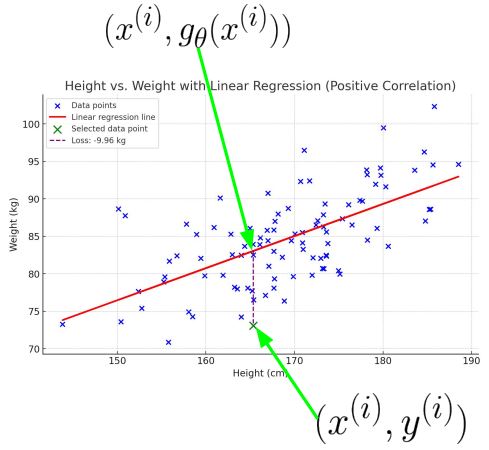
하나의 데이터 $x^{(i)}$에 대해서 생각해보자. 함수 f*에 따른 출력은 $y^{(i)}$이어야 한다. 그리고 g함수의 출력은 $g_{\theta}(x^{(i)})$ 이다. 이 둘의 근사도는 오차 계산방법인 MSE(Mean Square Error)로 계산할 수 있다.

\[\begin{align*} loss &= l(g_{\theta}(x^{(i)}), y^{(i)}) \\ &= (g_{\theta}(x^{(i)}) - y^{(i)})^2 \end{align*}\]

따라서 모든 입력 데이터에 대한 MSE는 다음과 같이 계산된다.

\[L(\theta) = \sum_{i=1}^n (g_{\theta}(x^{(i)}) - y^{(i)})^2\]

MSE는 왜 절댓값이 아닌 제곱을 사용할까?
제곱을 하면 큰 오차에 대해 더 큰 패널티를 부여할 수 있고 미분이 가능하기 때문에 계산에 용이하다.

MSE(회귀 문제에 주로 사용)외에도 cross-entropy(분류 문제에 자주 사용)와 같이 상황에 맞게 다른 오차 계산법을 사용할 수 있다. $L(\theta)$를 최소로 만드는 a, b의 값은 편미분(gradient)를 통해서 구할 수 있다. multidimension에서도 마찬가지로 편미분으로 구할 수 있다.

Multi-dimension에서의 손실함수?
데이터를 $x = (x_1, x_2, …, x_d)$라고 하면 G함수는 $a^Tx+b$ 형태를 가진다.이때 b를 1xb로 해석하면, $x=(1, x_1, x_2, …, x_d)$이고 G 함수는 $a^TX$로 표현할 수 있다. (이때, $a=(a_0, a_1, …, a_d)) 그러면 손실 함수는 다음과 같이 정의할 수 있다.

\[\begin{align*} L(a) &= \sum_{i=1}^n (g_{a}(x^{(i)}) - y^{(i)})^2 \\ &= \left\| \begin{bmatrix} a^Tx^{(1)}-y^{(1)} \\ a^Tx^{(2)}-y^{(2)} \\ ... \\ a^Tx^{(n)}-y^{(n)} \end{bmatrix} \right\|^2 \\ &= || Xa - Y ||^2 \\ &= Y^TY - 2Y^TXa + a^TX^TXa \end{align*}\]

또한 손실 함수를 최소로하는 a의 값에 대한 식은 아래와 같이 정리할 수 있다.

\[\frac{\partial L(a)}{\partial a} = -2X^TY + 2X^TXa = 0 \\ \therefore a = (X^TX)^{-1}X^TY\]

위의 식을 통해서 다른 문제에서도 a값을 쉽게 구할 수 있다.

2-2. 다차원 모델

만약 선형 함수가 아니라 2차, 3차 함수로 모델을 생성하고 싶다면 어떻게 될까? 예를 들어 $X’=(1, x, x^2)$이라고 하자 그러면 $g_a(x) = a_0+a_1x+a_2x^2 = aX’$과 같이 정의할 수 있을 것이다. 우리가 구하고자 하는 것은 a이므로 x의 차수가 변하더라도 a_1, a_2, …의 입장에서는 여전히 일차 함수인 셈이다. 따라서 위와 동일한 방식으로 행렬 a의 값을 구할 수 있다. 이처럼 모델의 차수가 커질수록 더 많은 것을 표현할 수 있지만 항상 오버피팅에 주의해야 한다.

오버 피팅 해결법?

• 모델의 복잡도 낮추기
• 데이터 추가하기 (생성 모델 사용, 증강)
• 규제

2-3. 경사 하강법(Gradient Descent, GD)

손실함수를 최소화하는 가중치들의 값을 구할 때, 우리는 편미분의 조합을 통해서 구할 수 있었다. 하지만 모델의 파라미터가 매우 많거나 복잡한 손실함수 사용으로 인해 계산이 어려울 수 있다. 그때, 경사 하강법으로 최적의 가중치 값들을 근사할 수 있다.

경사하강법은 우리가 model의 global view는 모르지만(=모델의 최솟점이 어디인지 모르지만) 현재의 gradient 값은 안다고 가정한다. 그리고 현재의 gradient 방향 즉, 현재의 위치에서 가장 급한 기울기 방향으로의 이동을 반복해 기울이가 0인 지점으로 근사한다. 한번에 이동하는 크기는 learning rate로 조절한다.

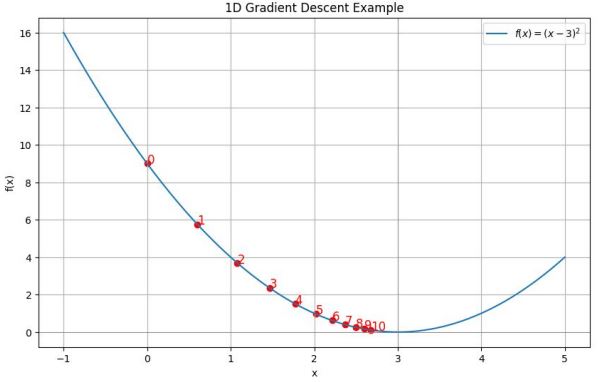
예를 들어, $f(x) = (X-3)^2$의 모델에서 최솟값을 찾는다고 하고, 초기 위치를 $x_0 = 0$, learning rate를 $\alpha=0.1$이라 하자. 그러면 현재 위치에서 가장 급한 기울기는 $f’(0)=2(0-3)=-6$이다.

\[\begin{align*} x_{i+1} &= x_i - \alpha \nabla L(x_i) \\ &= 0 - 0.1 \times (-6) = 0.6 \end{align*}\]

따라서 다음에는 $x = 0.6$ 의 위치에서 다시 gradient 방향으로의 이동을 시도한다. 이를 계속 반복하면 기울기가 0인 $x=3$에 도달할 수 있다.

이때 이동 크기를 결정하는 learning rate $\alpha$의 값이 너무 작으면 최솟값에 도달하기까지 많은 시간이 소요된다. 반대로 $\alpha$가 크면 빠르게 이동 가능하나 너무 큰 값을 부여한 경우에는 이동 범위가 너무 커, 최솟점에 도달하지 못하고 발산하는 경우가 생긴다. 따라서 적절한 값의 $\alpha$를 사용해야 한다.

Learning rate 스케쥴링 방법?
기본적으로 목적지에 도달할수록(일정 스텝마다) lr를 줄인다.

1. 기본 스케쥴링
   매 s번째 epoch마다 $\alpha := \alpha \times d$ 로 업데이트
2. Exponential 스케쥴링
   매 epoch 마다 $\alpha := \alpha_{0} \times \exp^{-\gamma t}\;(\gamma \text{는 decay rate, t는 epoch})$ 로 업데이트
3. Adaptive 스케쥴링(Annealing)
   $L_{val} \geq L_{best}$ 일때에만 patient counter k 를 증가시키고 $k \geq p$ 이때에, $\alpha := \alpha \times d$로 업데이트한다. 즉, 발산하는 양상을 보일 때, $\alpha$값을 업데이트 한다.

2-4. 확률적 경사 하강법(Stochastic Gradient Descent, SGD)

일반적으로 손실함수는 모든 데이터의 손실의 평균으로 정의된다. 하지만 모든 데이터에 대해 계산하려면 그 만큼 계산의 비용이 크다. 이를 해결하기 위해 하나의 데이터의 손실을 해당 iteration의 손실함수로 사용하는 방법을 확률적 경사 하강법이라 한다. 실제 손실함수의 gradient가 아니기 때문에 noisy하지만 계산적 이득이 훨씬 크다.

• Gradient Descent에서의 gradient 계산

\[\nabla L(\theta) = \frac{1}{n} \sum_{i=1}^n \nabla l(g_{\theta}(x^{(i)}), y_i)\]

• Stochastic Gradient Descent에서의 gradient 계산

\[\nabla L(\theta; x^{i}, y^{i}) = \nabla l(g_{\theta}(x^{(i)}), y_i)\]

하나의 데이터로는 노이즈가 커, 불안정하기에 여러 개의 데이터를 이용하여 손실함수를 정하는 방법을 mini-batch Gradient Descent라고 한다. 경사하강법보다 계산이 빠른 동시에 안정성을 가진다.

• Mini-batch Gradient Descent에서의 gradient 계산

\[\nabla L(\theta; B) = \frac{1}{b} \sum_{i \in B} \nabla l(g_{\theta}(x^{(i)}), y_i)\]

2-5. Local minima

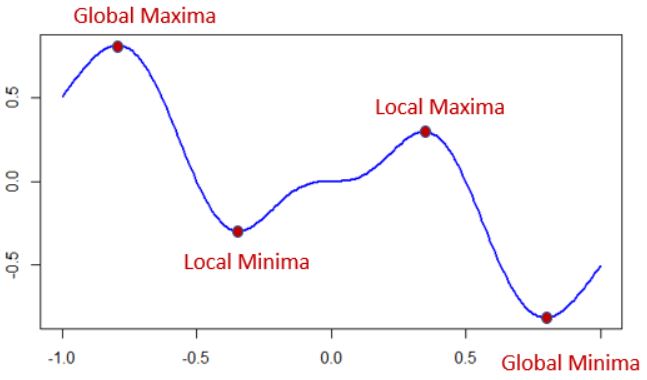
경사 하강법들의 가장 큰 문제점은 local minima에 빠질 수 있다는 점이다. 목적함수는 기울기가 0이 되는 지점을 여러개 가질 수 있는데, 그 중 가장 낮은 부분을 global minima, 나머지를 local minima라고 한다. 경사 하강법은 현재 위치에서 보이는 가장 낮은 부분으로 이동하기에 초기값에 따라 local minima로 수렴할 수도 있다. 혹은 평평한 지대(plateau, 플래토)에도 빠질 수도 있다.

이를 해결하기 위해서 모멘텀 SGD(Momentum SGD)가 개발되었다. 매 지점에서 가장 가파른 방향으로 이동하는 것이 아니라 어떠한 gradient로 어떠한 궤적을 따라 내려왔는지를 고려한다. 즉, 이동 방향을 현재 위치에서의 gradient와 지금까지의 gradient의 총합의 선형 결합으로 표현된다.

\[v_t = \beta v_{t-1} + (1-\beta) \nabla L(\theta_{t-1})\;(0 \le \beta \ge 1) \theta = \theta_{t-1} - \alpha v_t\]

• $\beta$가 더 작을수록 현재의 gradient에 더 의존

관성(Momentum)을 가지기 때문에 이는 local minima에서 빠져나올 수 있도록 도와준다.

또한 gradient의 크기가 너무 크거나 작아지는 문제를 완화하기 위해 gradient의 값을 교정하는 방법으로는 RMS Prop가 있다. gradient의 각 위치에서의 크기 값에 따라 정규화함으로써 gradient값을 계산한다.

모멘텀 SGD와 RMP Prop을 합친 기법을 ADAM이라고 하며, 실제 자주 사용된다.

참고

본 포스팅은 LG Aimers 강좌 중 연세대학교 노알버트 교수님의 ‘지도학습’에서 학습한 내용을 정리한다.

i2 tutorials의 What are Local Minima and Global Minima in Gradient Descent?