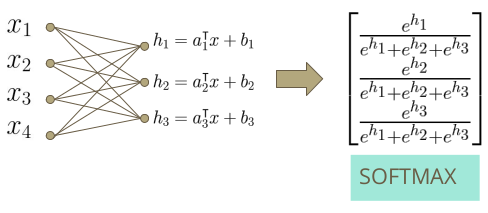[AI] 지도 학습2
지도학습 중 분류에 대해 자세히 알아본다.
회귀에 이어, 분류 모델의 학습 과정에 대해 자세히 살펴보자.
1. 분류(Classification)
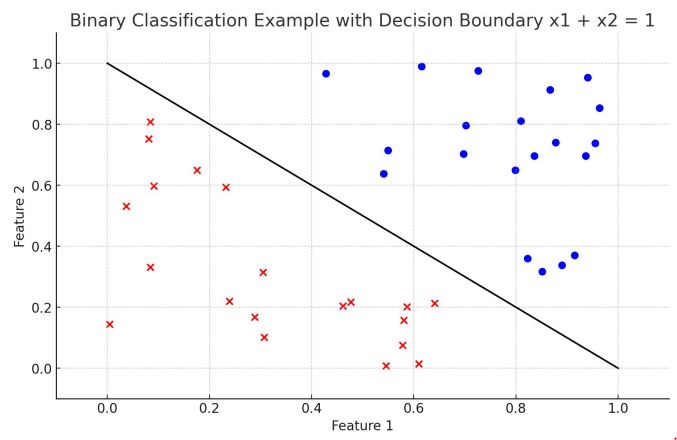
먼저 분류 모델 중 가장 간단한 Binary Classification의 예로 설명해보고자 한다. 이 모델은 예측 결과를 두 개의 집단으로 분류하는데, 데이터들을 선형적으로 구분 가능하다고 가정한다. 즉, 데이터를 완벽히 나누는 선 혹은 hyperplane이 하나 이상 존재한다고 가정한다. 분류 모델 역시, 회귀와 마찬가지로 함수 클래스 G 중에 정답 함수 f*에 가장 근접한 함수 g를 찾는 것을 목표로 한다.
데이터들이 $x^{(i)} = (x_1^{(i)}, x_2^{(i)})$ 형태로 주어지고 예측 결과는 $y^{(i)} \in {-1, 1}$이 된다.
\[L(y, \hat{y}) = \begin{cases} 0, &\text{if}\;y = \hat{y} \\ 1, &\text{if}\;y \neq \hat{y} \end{cases}\]분류의 경우에는 0/1 loss 방법으로 손실함수를 정의하는데, 각 데이터에 대해 예측이 틀린 경우에는 손실 값을 1, 맞은 경우에는 손실 값을 0으로 주는, 정답의 개수를 카운팅하는 함수이다.
Binary classification은 퍼셉트론 알고리즘으로 풀 수 있다.
퍼셉트론 알고리즘(Perceptron Algorithm)?
\[\begin{align*} & a \leftarrow a + \eta (y_i-\hat{y_i})x_i \\ & b \leftarrow b + \eta (y_i-\hat{y_i}) \end{align*}\]
$g = a^{T}x + b$라고 하면, 각 데이터에 대한 예측이 틀릴 때마다 $(y \neq \hat{y})$ 아래 수식으로 가중치와 bias를 업데이트 한다. 아래 식에서 $\eta$ 는 학습률(learning rate)이다.
하지만 퍼셉트론 알고리즘은 정답 함수가 있다고 가정할 때 사용될 수 있다. 만약 정답 함수가 없다면, 퍼셉트론 알고리즘은 멈추지 않고 무한히 동작할 것이다. 문제는 이것이 정답 함수가 없어서 알고리즘이 무한 반복되는 것인지, 정답 함수로 향해가는 중인지를 구분할 수 없다는 것이다.
1-1. SVM(Support Vector Machine)
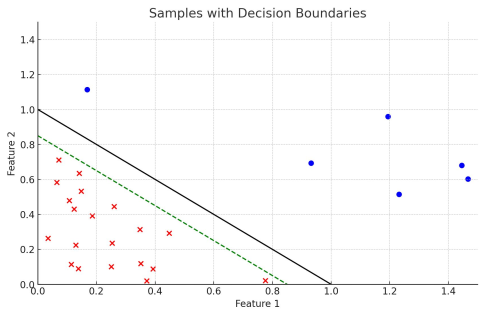
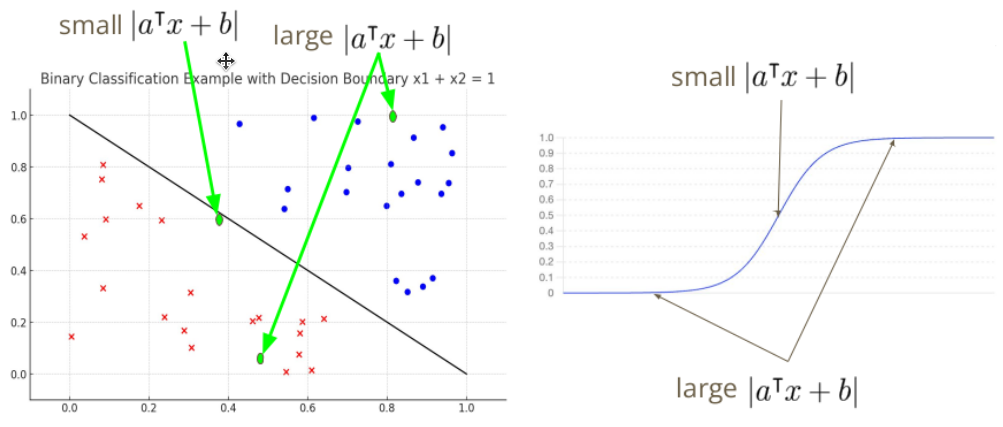
그러면 위의 binary classification 문제를 조금 다듬어보자. 기존의 binary classification은 예측 $ax_i+ b$에 따라 클래스 $y_i$의 값이 결정되었다. 하지만 이 둘을 곱하게 되면 목적은 없고 제약조건만 있는 문제로 변환이 된다. 즉, $y_i(ax_i+b) > 0$을 풀면 된다. 이 식을 사용하면 정답의 존재 여부를 빠르게 판단할 수 있다. 하지만 이를 만족하는 $ax+b$는 매우 많다.
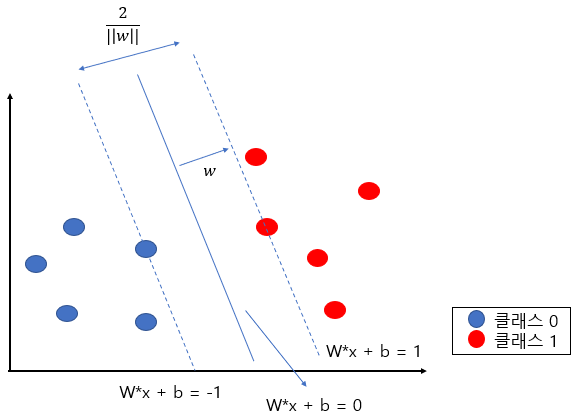
위의 이미지에서 파란점과 빨간x를 분류하는 선에 대해서 초록색 보다는 검은 실선이 더 좋은 분류선으로 보인다. 이처럼 분류 직선이 데이터로부터 적절한 거리를 유지하는 경우에 일반화가 더 잘된 모델이라고 할 수 있다. 분류 직선과 데이터 점들 사이의 거리를 마진(Margin)이라고 하며, 아래 수식을 통해 계산할 수 있다.
\[d_i = \frac{|a^Tx_i + b|}{||a||} \;(x_i와\;직선 a^T+b =0\;사이의\;거리)\]그리고 모든 데이터에 대해 마진을 최대로하는 분류 직선을 구하는 알고리즘으로는 SVM(Support Vector Machine)이 있다. 위의 거리 식에서 계산을 단순히 하기 위해, $|a^Tx_i +b|$를 1로 고정하자.
그러면 결국 모든 데이터에 대해 $y^{(i)}(ax^{(i)}+b) \ge 1$이면서, 마진의 크기 $\frac {||a||^2}{2}$를 최소로 하는 a, b의 값을 찾는 문제로 바꿀 수 있다.
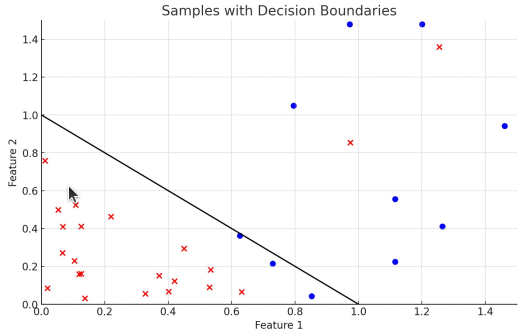
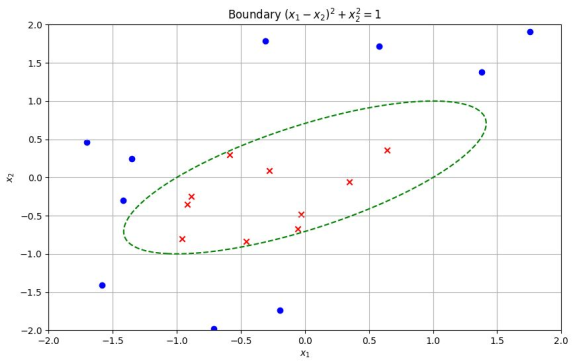
하지만 만약 위 그림과 같이 두 클래스를 완벽히 분류하는 정답 함수가 없는 경우라면 어떻게 해야 할까?
그럴때는 소프트 마진 SVM(soft-margin SVM)을 사용할 수 있다. 기존의 SVM과 유사하지만 넘어가는 데이터에 대해 약간의 penalty(slack variable)를 추가한다.
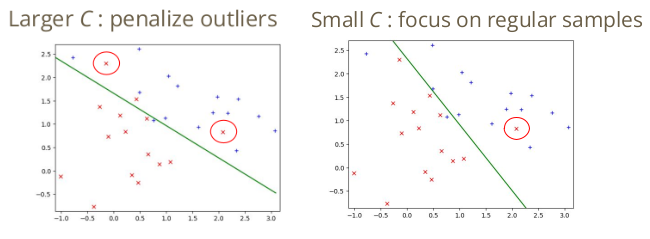
\[y^{(i)}(ax^{(i)}+b) \ge 1 - \zeta \;이면서\;\frac{||a||^2}{2} + C\sum_{i=1}^n \zeta _i\;를\;최소화\]$\zeta _i \ge 0$이면서 C값이 클수록 분류 직선의 범위를 넘어가는 것(이상치, outlier)에 대해 패널티를 크게 준다. 아래의 그림은 C값에 따라 동일한 데이터를 어떻게 분류하는지 보여준다.
소프트 마진 SVM을 hinge loss를 사용하면 아래와 같이 식을 더 간단하게 변경할 수 있다.
\[\frac{1}{2} ||a||^2 + C \sum_{i=1}^n L(y_i, f(x_i)) \\ L(y_i, f(x_i)) = max(0, 1-y_i(a^Tx_i + b))\]Hinge Loss?
0 과 $1-\hat{y}y_i$ 중에 값이 더 큰 것을 사용하는 손실함수이다.
소프트 마진 SVM에서 $\zeta \ge 0$이고, $\zeta \ge 1-y_i(a^Tx_i+b)\;(\leftarrow y^{(i)}(ax^{(i)}+b) \ge 1 - \zeta$의 변형) 이므로 $\;max(0, 1-y_i(a^Tx_i + b))$로 적을 수 있다.
직선이 아닌 더 복잡한 함수로 분류를 해야한다면 $x_i^2$, $x_i^3$과 같이 다차원으로 확장할 수 있을 것이다. 하지만 이 경우 역시, 회귀와 마찬가지로 오버피팅의 가능성을 고려해야한다.
1-2. 로지스틱 회귀(Logistic Regression)
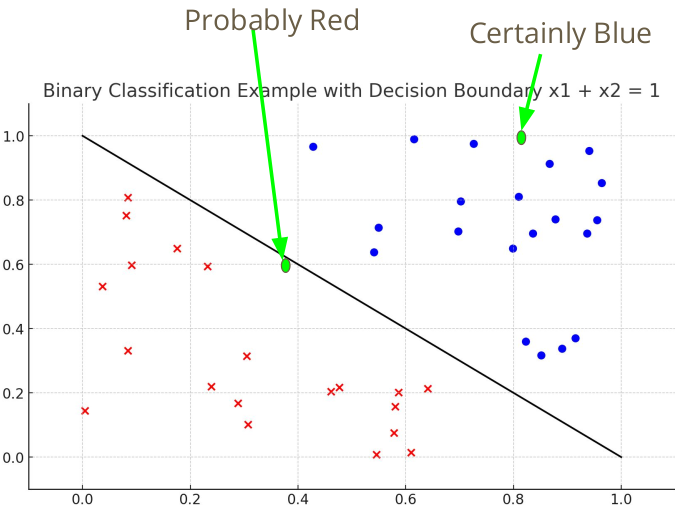
이때까지는 데이터는 -1 혹은 1 클래스로 분류하였다. 하지만 위의 그림과 같이 두 초록점이 주어졌을 때, 분류 직선의 거리에 따라 에측에 대한 신뢰도를 함께 생각해볼 수 있다. 그리고 이 신뢰도는 확률값으로 표현할 수 있다.
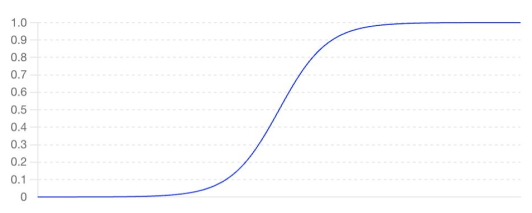
\[\sigma(x) = \frac{1}{1+e^{-x}}\]로지스틱 함수는 입력 값을 0과 1사이의 값으로 변환해주는 함수로, 이를 이용해 이진 분류 문제를 해결하는 모델을 로지스틱 회귀(Logistic Regression)이라고 한다. 로지스틱 회귀는 주어진 입력을 0과 1 사이의 출력(입력값에 대한 확률)으로 변환한다. 즉 아래와 같이 각 점을 해석한다.
로지스틱 회귀의 모델을 아래와 같이 정의할 수 있다.
\[g_{a,b}(x) = \begin{bmatrix} Pr(y = -1) \\ Pr(y = 1) \end{bmatrix} = \begin{bmatrix} 1-\sigma(x) \\ \sigma(x) \end{bmatrix} = \begin{bmatrix} \frac{e^{-(a^Tx+b)}}{1+e^{-a^Tx+b}} \\ \frac{1}{1+e^{-a^Tx+b}} \end{bmatrix}\]1-3. Cross Entory Loss
이제 로지스틱 회귀 모델에 대한 손실을 정의해보자. 우리가 강수 확률이 70%일 때 비가 온 것과 강수 확률이 30%일 때 비가 온 것 사이에 손실을 다르게 부여해야 한다. 다시 말하면, 확률이 클수록 그에 대한 손실이 작아야 한다.
\[l(g_{a,b}(x^{(i)}), y^{(i)}) = log \frac{1}{\hat{y}(y^{(i)})}\]Cross entropy loss는 KL Divergence 혹은 Relative Entropy라고 하는 식에서 유도되었다.
KL Divergence(Relative Entropy)?
두 개의 확률분포가 얼마나 멀리 떨어져 있는가(확률분포 사이의 거리)를 계산하는 함수이다.
클래스가 1 일때와 -1일 때 모두 적용할 수 있는 로지스틱 회귀에서 손실함수는 아래와 같이 표현할 수 있다.
\[L(\theta) = -\frac{1}{n} \sum_{i=1}^n \begin{bmatrix} \frac{1+y^{(i)}}{2} log(g_\theta(X^{(i)})) + \frac{1-y^{(i)}}{2} log(1-g_\theta(X^{(i)})) \end{bmatrix}\]위의 식에서 $g_\theta(x) = 1+e^{-\theta^Tx}$를 대입하여 정리하면 아래와 같다.
\[\begin{align*} &-log\;g_\theta(X^{(i)}) = log(1+e^{-\theta^Tx}) \\ &-log\;(1-g_\theta(X^{(i)})) = log(1+e^{\theta^Tx}) \\ &\therefore L(\theta) = \frac{1}{n} \sum_{i=1}^n log(1+e^{-y^{(i)}\theta^TX^{(i)}}) \end{align*}\]2. 다중 분류(Multiclass Classification)
클래스가 여러개인 경우에는 이진 분류의 일반화로 문제를 해결할 수 있다. 예를 들어 비행기, 자동차, 배를 구분하는 문제에서 각 이미지가 비행기인지 아닌지, 자동차인지 아닌지처럼 이진 분류를 여러번 반복해서 풀 수 있다.
하지만 소프트맥스 회귀(softmax regression)를 사용하면 로지스틱 회귀와 비슷한 형태로 문제를 풀 수 있다.
2-1. 소프트맥스 회귀
소프트맥스 회귀는 로지스틱 함수 대신에 소프트맥스 함수를 사용한다. 먼저 각 클래스를 잘 표현하는 선형함수를 찾고 이 값을 exponential 함수를 취하고 정규화해, 확률분포 형태로 만들어준다. 즉, 소프트맥스를 거친 확률들의 합은 1이되고, 모두 양수이다.
이 모델 역시 cross entropy loss를 사용해 평가할 수 있다.
2-2. 한계점(Threshold, 기준점) 설정
확률을 평가할 때, 예측에 대한 기준점을 잘 설정해야 한다. 예를 들어, 어떤 사람이 코로나가 걸렸을 확률이 30%, 안 걸렸을 확률이 70%일 때, 코로나에 대해 엄격히 하고 싶다면 30%의 확률인 사람도 코로나로 간주하고 추가적인 검사를 제안하는 것이 좋다.
하지만 기준점을 너무 낮게 설정하면, 실제로 코로나가 걸리지 않은 사람도 코로나 양성으로 판단하는 False Positive 값이 커질 수 있다. 반대로 기준점을 너무 높게 설정한다면 코로나가 걸린 사람을 코로나 음성이라고 판단하는 False Negative가 발생한다.
이를 사용해, 양성이라 판단한 사람 중에 실제 양성이 있었던 비율을 Precision이라 하고, 실제 양성 중에 얼마나 양성으로 판단했는지에 대한 비율을 recall이라 한다.
\[Precision = \frac{tp}{tp+fp} \\ recall = \frac{tp}{tp+fn}\]이 둘은 서로 trade-off 관계를 가지기 때문에, 각자 상황에 모델에 threshold를 적용하면 된다. 만약 이 두 값이 적절히 조화로운 모델을 사용하고 싶다면 precision과 recall의 조화 평균인 F1-score를 사용할 수 있다.
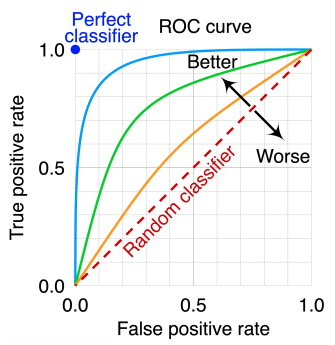
또, 좋은 모델인지 평가하기 위해서 ROC Curve를 사용할 수도 있다.
- True Positive Rate(TPR) = TP/(TP+FN)
- False Positive Rate(FPR) = FP/(FP+TN)
완벽한 분류 모델의 경우에는 TPR을 1, FPR을 0으로 가져야한다. 하지만 이 둘 역시 trade-off 관계를 가진다. 하지만 이 둘이 trade-off를 가지는 곡선의 형태가 파란점에 가깝게 굽은 곡선일수록 즉, ROC Curve의 크기가 클수록 더 좋은 모델이다.
3. 데이터
일반적으로 학습 데이터를 학습, 검증 데이터로 분리해 학습을 한다.
- 학습:검증을 8:2로 주로 설정한다. 학습 데이터와 검증 데이터 그리고 테스트 데이터의 관계를 연습 문제, 모의 고사, 수능으로 생각하면 이해하기 쉽다. 학습 데이터로 학습을 하다가 검증 데이터로 overfitting이 발생하지 않았는지 확인한다. 그리고 모델의 최종적인 성능은 테스트 데이터로 판단이 된다.
3-1. 교차 검증(cross validation)
validation error가 train error보다 살짝 크다면 적절히 학습이 된 것이고, 둘 사이의 차이가 크다면 overfitting일 가능성이 크다.
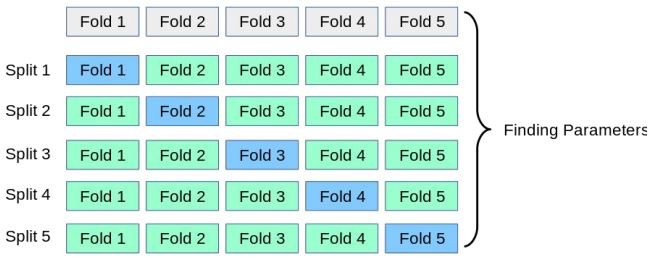
만약 데이터의 양이 적어 학습 데이터와 검증 데이터를 나누기 어렵다면 교차 검증 방법을 사용할 수 있다.
- 학습 데이터 양이 작아도 오버피팅이 될 가능성이 높다.
예를 들어 학습 데이터를 총 5개의 그룹으로 나누고 한번은 첫 번째 그룹을 검증 데이터로 사용하고, 다음번엔 두번째 그룹을 검증 데이터로 사용한다. 이처럼 매 iteration마다 번갈아가면서 특정 그룹을 검증 데이터로 활용하는 방법을 교차 검증이라 한다.
3-2. 증강(Augmentation)
강아지 사진을 이동, 회전, 뒤집어도 여전히 강아지 사진이다. 이처럼 데이터에 다양한 변환(회전, 이동, 확대, 축소, 뒤집기 등)을 적용해 새로운 데이터를 생성하는 방법이다. 하지만 숫자 2와 같이 변환으로 인해 데이터의 성질이 변화되는 경우가 있을 수도 있으니 주의해야 한다.
참고
본 포스팅은 LG Aimers 강좌 중 연세대학교 노알버트 교수님의 ‘지도학습’에서 학습한 내용을 정리한다.