[RL] FrozenLake에서 Q Network 학습하기
Q Network를 사용하여 FrozenLake를 학습해본다.
Q 테이블을 이용한 학습은 성능이 좋지만, 상태(state) 공간이 커지면 테이블 크기가 커져 실생활 적용엔 무리가 있다. 따라서 이번 포스팅에서는 Neural Network를 이용해 학습을 해보고자 한다.
1. Neural Network(인공 신경망)
인공 신경망은 두뇌의 뉴런을 모방한 모델이다. 마치 하나의 뉴런이 다른 여러 뉴런으로부터 입력 신호를 받아 출력 신호를 내보내는 것처럼 인공 신경망은 입력 값을 받아 처리 후 출력 값을 내보낸다.
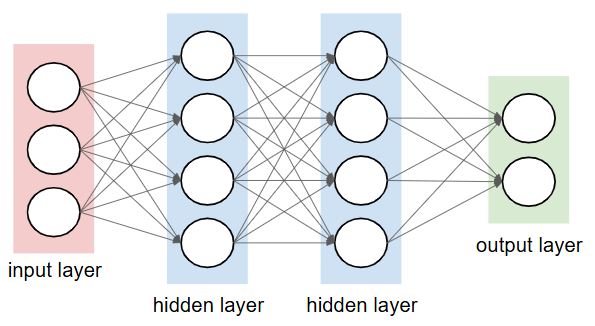
인공 신경망은 여러개의 층(layer)를 쌓아서 만들 수 있는데, 입력을 받는 곳을 입력층(input layer), 데이터 처리 및 학습이 일어나는 곳을 은닉층(hidden layer), 최종 결과를 내는 곳이 출력층(output layer)이다. 하나의 인공 신경망은 여러개의 은닉층을 가질 수 있으며, 은닉층이 많아질수록 학습 능력이 증가하지만, 계산 복잡성과 과적합 위험이 높아질 수 있으므로 적절한 균형이 필요하다.
신경망이 학습을 잘 진행하고 있는지 평가하는 함수를 cost 함수라 하는데, 이는 예측값과 실제값(정답) 사이의 차이를 측정하는 방식으로 정의된다. 아래는 cost 함수 종류 중의 하나인 MSE(Mean Square Error, 평균 제곱 오차)이다.
\[cost(W) = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \quad (n은\;데이터의\;수)\]2. Q Network
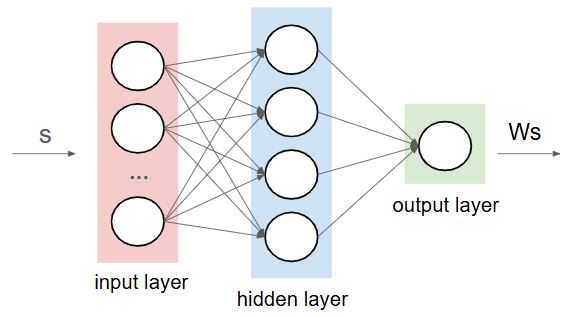
강화학습에서 사용되는 신경망 기반 학습 알고리즘을 Q Network라 한다. FrozenLake에서는 state를 입력으로 넣고 그에 따른 action을 출력하는 신경망을 구성할 수 있다.
입력을 s, 각 레이어들의 가중치의 집합을 W라 하면 출력은 Ws가 된다. 이 Ws가 Q 테이블에서의 Q(s, a)와 같으므로 이 Ws가 최적의 Q 값(y)을 갖는 방향으로 학습을 해야한다. 그러므로 cost 함수는 아래와 같이 정의할 수 있다.
\[cost(W) = \frac{1}{m} \sum_{i=1}^{m} (Wx^{(i)} - y^{(i)})^2\]Q 테이블에서 y의 값을 $r +\gamma\;maxQ(s’, a’)$로 정의했었다. cost 함수의 평균을 아래와 같이 다시 표현할 수 있다.
\[\begin{align*} cost(W) &= \frac{1}{m} \sum_{i=1}^{m} (Wx^{(i)} - y^{(i)})^2 \\ &= \frac{1}{m} \sum_{i=1}^{m} (\hat{Q}(s_i, a_i) - r_i + \gamma\;max_{a'} \hat{Q}(s_{t+1}, a'))^2 \\ \end{align*}\]그리고 이 cost 함수를 최소화하는 파라미터들의 집합 $\theta$를 구해야한다.
2-1. 가중치(W)와 파라미터($\theta$)의 차이
정확히 말하자면, 가중치 W는 신경망에서의 가중치 행렬을 의미한다. 입력 x와 출력 y간의 관계를 $y=Wx+b$와 같은 형태로 표현하며, 각 레이어마다 고유한 W값을 갖는다. 입력된 데이터들을 W를 통해 각각 다른 비중으로 다음층에 전달한다.
파라미터 $\theta$는 모델이 데이터로부터 학습 가능한 값들을 말한다. 여기에는 가중치 W 뿐만 아니라 편향(bias)도 포함되어 있다.
2-2. Stochastic?
신경망을 학습시키기 위해서 Q 함수로 $r +\gamma\;maxQ(s’, a’)$를 사용하였다. 하지만 해당 수식은 stochastic이 아니라 deterministic한 환경에서 사용하는 수식이다.
왜 deterministic 환경에서의 수식을 사용하는 것일까? Stochastic한 함수를 새로 정의했던 이유를 다시 생각해보자.
Stochastic 환경에서는 action에 따른 결과가 불안정했다. 그렇기에 Q 함수가 업데이트 될 때 값이 한번에 학습되는 것이 아니라, 원래의 값을 유지하면서 조금씩 학습을 받아들이도록 수식을 변형하였다.
인공 신경망은 cost 함수를 통해 조금씩 학습하므로 식을 변형하지 않고 deterministic의 수식을 사용해도 동일한 효과가 나타낸다.
3. 실습(Q Network)
간단한 실습을 위해 가장 기본적인 선형 회귀(Linear Regression)로 작성하며, bias가 0인 $y=Wx$ 수식을 사용한다.
먼저 필요한 패키지들을 import 한다.
1
2
3
4
5
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
import gym
from gym.envs.registration import register
입력으로는 state가 전달되어야 한다. 하지만 1, 3과 같이 state값 자체를 전달하기 보다는 쉬운 계산을 위해 one hot encoding 방식으로 입력 X를 전달하고자 한다.
1
2
3
4
5
6
7
8
9
input_size = env.observation_space.n
def one_hot(x, size):
return np.identity(size)[x:x+1] # 단위 행렬의 x행을 반환
X = tf.Variable(tf.ones(shape=[1, input_size], dtype=tf.float32)) # 입력 행렬의 크기 정의
# 추후 사용시 아래와 같이 입력 정의
X.assign(one_hot(state, input_size))
가중치와 사용할 최적화 알고리즘을 정의한다. 해당 실습에서는 SGD(Stochastic Gradient Descent, 확률적 경사 하강법)를 사용한다.
1
2
3
4
5
6
7
input_size = env.observation_space.n
output_size = env.action_space.n
learning_rate = 0.1
# W는 0~0.01 사이의 값을 임의로 부여한 [input_size, output_size] 크기의 행렬
W = tf.Variable(tf.random.uniform([input_size, output_size], 0, 0.01))
optimizer = tf.keras.optimizers.SGD(learning_rate=learning_rate)
입력된 state에 대해 적절한 action을 선택하도록 $\hat{y}$를 $y$에 근사하는 방향으로 학습한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
dis = 0.99 # discount factor
s = env.reset()[0]
done = False
while not done:
X.assign(one_hot(state, input_size))
with tf.GradientTape() as tape:
Qpred = tf.matmul(X, W) # [1, input_size] * [input_size, output_size] = [1, output_size]
// action 선택 코드
new_state, reward, done, truncated, info = env.step(a)
if done:
Qs = Qpred.numpy()
Qs[0, a] = reward # Qs는 [1, output_size] 크기이므로 index 0을 통해서 먼저 접근해야 한다.
else:
X.assign(one_hot(new_state, input_size))
Qnexts = tf.matmul(X, W)
Qs = Qpred.numpy()
# 값 업데이트
Qs[0, a] = reward + dis * tf.reduce_max(Qnexts)
# 손실 함수 정의
loss = tf.reduce_sum(tf.square(Qs - Qpred))
# 그래디언트 계산 및 가중치 업데이트
grads = tape.gradient(loss, [W])
optimizer.apply_gradients(zip(grads, [W]))
action 선택은 앞서 배운 e-greedy 방식을 사용하여 작성할 수 있다.
1
2
3
4
5
6
e = 1. / ((i / 50) + 10)
if np.random.rand(1) < e:
a = env.action_space.sample()
else:
a = tf.argmax(Qpred[0]).numpy()
해당 학습을 num_episode만큼 반복한다.
1
for i in range(num_episodes):
최종 코드는 여기서 확인 할 수 있다.
3-1. 실행 결과
Success rate 0.533으로 Q 테이블을 활용한 학습보다 좋지 않은 성능을 보인다.
참고
Sung Kim 강사님의 모두를 위한 RL