[RL] FrozenLake Q-table 사용하기

이번 포스트에서는 Q-function 개념을 소개하고, Q-table 방식을 사용하여 FrozenLake를 학습해본다.

1. Q-function

컴퓨터가 FrozenLake 게임을 진행할 때, 현재 상태에 대해 어떤 action을 선택하는 것이 좋을까?

먼저 랜덤으로 action을 선택하는 방법이 있다. 하지만 어떠한 방향에 구멍(H)이 있는지 알 때에는 랜덤으로 선택하는 것보다 구멍이 아닌 방향으로 action을 취하는 것이 좋다. 이처럼 현재 상태에서의 각 action에 대한 퀄리티(얻을 수 있는 예상 최대 보상값)를 반환해주는 함수를 Q-function이라고 한다. Q-function은 Q(state, action) 형태로 작성한다.

예를 들어 아래와 같이 Q-function이 주어졌다고 하자.

\[\begin{align*} &Q(s, LEFT) = 0 \\ &Q(s, RIGHT) = 0.8 \\ &Q(s, UP) = 0.2 \\ &Q(s, DOWN) = 0.6 \end{align*}\]

그러면 에이전트는 s상태에서 얻을 수 있는 보상이 제일 큰 action=RIGHT를 선택한다.

2. Q-function의 수학적 표기

현재 상태 s에서 a를 선택했을 때 다음 상태를 s’이라고 하면 Q-function은 a를 통해 얻은 reward와 다음 상태에서의 얻을 수 있을 최대 보상의 합으로 생각할 수 있다. 이를 수학적으로 recursive하게 표현하면 아래와 같다.

\[\hat{Q}(s, a) \leftarrow r + max_{a'} \hat{Q}(s', a') \quad (a'은\;s'에서의\;보상을\;최대화하는\;action)\]

3. Q-table 계산하기

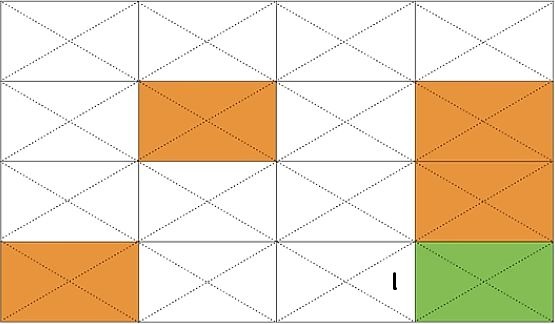
위의 그림에서 초록색은 목적지(G)를, 주황색은 구멍(H)을 그리고 흰색은 얼음(F)을 의미한다.

3-1. Q(s14, RIGHT)의 값을 구해보자.

s15가 목적지(G)이므로 얻을 수 있는 reward는 1이고, 다음 상태에서 취할 수 있는 action이 없으니 Q(s14, RIGHT) = 1 이라는 수식을 얻을 수 있다.

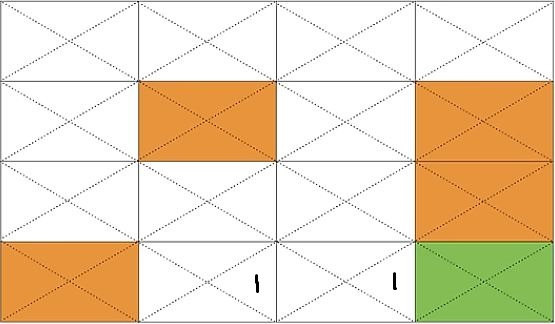
3-2. Q(s13, RIGHT)의 값을 구해보자.

s14에서 action=RIGHT로 얻은 reward는 0이고, 이후 상태에서 얻을 수 있는 최대 reward는 3-1에 의해서 1이므로 Q(s13, RIGHT) = 0 + 1 = 1 이다.

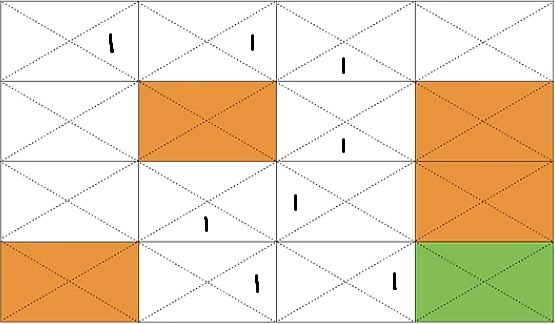
이와 같은 과정을 계속 반복해서 Q(s9, DOWN), Q(s10, LEFT), … , Q(s0, RIGHT)를 계산하면 아래와 같은 Q-table을 얻을 수 있다.

4. Q-table 실습(기본)

이전 코드에서 action 선택 부분을 수정하고 Q 테이블을 업데이트하는 부분을 추가해주면 된다. 먼저 Q 테이블을 초기화해주자.

Q = np.zeros([env.observation_space.n, env.action_space.n])

4-1. action 선택

현재 상태 s에서 Q(s, a)이 최대값이 되도록하는 action으로 선택하면 된다. 만약 최대값이 둘 이상이면 그 중에서는 랜덤하게 선택한다.

def rargmax(vector):
    m = np.amax(vector)
    indices = np.nonzero(vector == m)[0] # 최대값과 같은 요소에 True, 나머지는 False한 1차원 배열
    return random.choice(indices)

...

action = rargmax(Q[state, :])

4-2. Q 테이블 업데이트

수식 $\hat{Q}(s, a) \leftarrow r + max_{a’} \hat{Q}(s’, a’) $ 를 아래와 같이 코드로 작성한다.

Q[state, action] = reward + np.max(Q[new_state, :])

반복 수행을 통해 학습(최적의 Q table 완성)이 이루어질 수 있도록 해당 동작을 num_episodes만큼 반복한다.

num_episodes = 2000

for i in range(num_episodes):

최종적으로 전체 코드는 아래와 같다.

import gym
from gym.envs.registration import  register
import numpy as np
import matplotlib.pyplot as plt
import random

"""주어진 배열에서 최댓값을 가진 요소 중 랜덤으로 인덱스 반환"""
def rargmax(vector):
    m = np.amax(vector)
    indices = np.nonzero(vector == m)[0] # 최대값과 같은 요소에 True, 나머지는 False한 1차원 배열
    return random.choice(indices)

register(
	id = 'FrozenLake-v3',
	entry_point='gym.envs.toy_text:FrozenLakeEnv',
	kwargs= {'map_name':'4x4', 'is_slippery':False}
)

env = gym.make('FrozenLake-v3', render_mode='ansi')


# Q 테이블 생성
Q = np.zeros([env.observation_space.n, env.action_space.n])
num_episodes = 2000
# episode마다의 총 리워드
rList = []

for i in range(num_episodes):
    state = env.reset()[0]
    rAll = 0 # 리워드 총합
    done = False

    while not done:
        action = rargmax(Q[state, :])

        new_state, reward, done, truncated, info = env.step(action)
        
        Q[state, action] = reward + np.max(Q[new_state, :])
        
        rAll += reward
        state = new_state

    rList.append(rAll)
    
#최종 Q 테이블 출력
print("Final Q-Table Values")
print("LEFT DOWN RIGHT UP")
print(Q)
    
#시각화
print("Success rate: " + str(sum(rList)/num_episodes))
plt.bar(range(len(rList)), rList, color="blue")
plt.show()

4-3. 실행 결과

실행 결과 0.967로 높은 성공률을 보이며, 최종 Q 테이블은 아래와 같다. 코드에 random을 포함하고 있기에 실행 결과는 매번 달라질 수 있다.

순서대로 (LEFT,DOWN,RIGHT,UP)

\[\begin{align*} &[[0. 1. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.] \\ &[0. 1. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 0. 0.] \\ &[0. 0. 1. 0.][0. 0. 1. 0.][0. 1. 0. 0.][0. 0. 0. 0.] \\ &[0. 0. 0. 0.][0. 0. 0. 0.][0. 0. 1. 0.][0. 0. 0. 0.]] \end{align*}\]

5. 최적화

하지만 위의 방식이 항상 최적의 길을 찾는 것은 아니다. 항상 답이 보장되는(이미 시도해서 답을 알고 있는) 방향으로 가기보다는 가끔씩 새로운 방향을 시도해보는 것이 최적의 길을 찾는 중요한 단서가 된다.

이처럼 현재 있는 값을 이용하는 것을 exploit이라 하고, 새로운 시도를 한는 것을 exploration이라 한다.

5-1. e-greedy

대부분의 시도를 exploit로 선택하고 작은 e의 확률로 exploration을 시도하고 한다. 이러한 방식을 e-greedy(epsilon greedy) 알고리즘 방식이라 한다.

e = 0.1
if rand < e:
	a = random
else :
	a = argmax(Q(s,a))

5-2. Decaying e-greedy

시간이 지날수록 즉, 경험이 많이 쌓일수록 다양한 길이 이미 많이 시도되었을 가능성이 크다. 따라서 후반부로 갈수록 exploration의 확률 e를 더욱 줄인다.

for i in range(1000) :
	e = 0.1 / (i+1)
	if random(1) < e:
		a = random
	else :
		a = argmax(Q(s,a))

5-3. Random noise

e-greedy 방식 외에도 기존의 $Q(s, a)$에 랜덤한 가치(random_values)를 더한 후 action을 선택하는 방식을 통해 선택에 변화를 줄 수 있다. 마찬가지로 decaying을 적용할 수도 있다.

a = argmax(Q(s,a) + random_values)

# decaying 적용
for i in range(1000):
	a = argmax(Q(s,a) + random_values / (i+1))

5-4. Discount future reward

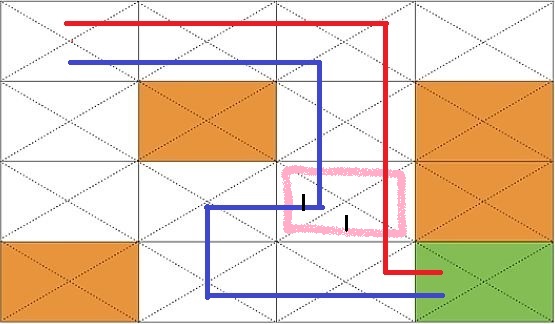
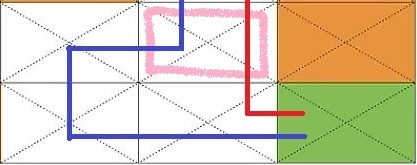
현재 에이전트가 분홍색 위치있다고 하자. 빨간색 길이 파란색 길보다 적은 이동 횟수로 목적지(G)에 도달하기에 빨간색의 방향인 아래로 향하는 것이 더욱 최적화된 길이다. 하지만 두 방향 모두 1의 reward를 가지기에 에이전트는 두 방향을 동일한 가치로 받아들인다.

\[\hat{Q}(s, a) \leftarrow r + \gamma \;max_{a'} \hat{Q}(s', a') \quad (\gamma<1)\]

위의 수식과 같이 현재 보상에 비해 나중의 보상의 가치를 낮추는 방식을 통해 두 방향에 차이를 둘 수 있다. 계산을 통해 이해해보자.

$\gamma = 0.9$라고 하면 아래와 같은 결과를 얻을 수 있다.

• 파란길

\[\begin{align*} &Q(s14, RIGHT) = 1 \\ &Q(s13, RIGHT) = 0 + 0.9*1 = 0.9 \\ &Q(s9, DOWN) = 0 + 0.9*0.9 = 0.81 \\ &Q(s10, LEFT) = 0 + 0.9*0.81 = 0.729 \end{align*}\]

• 빨간길

\[\begin{align*} &Q(s14, RIGHT) = 1 \\ &Q(s10, DOWN) = 0 + 0.9*1 = 0.9 \end{align*}\]

결과적으로 아래와 같은 Q 테이블을 얻을 수 있다.

따라서 에이전트는 분홍색 위치에 있을 때, reward값이 더 큰 action=DOWN을 선택하게 된다.

6. Q-table 실습(최적화)

최종적인 전체 코드는 아래와 같다.

import gym
from gym.envs.registration import  register
import numpy as np
import matplotlib.pyplot as plt

register(
	id = 'FrozenLake-v3',
	entry_point='gym.envs.toy_text:FrozenLakeEnv',
	kwargs= {'map_name':'4x4', 'is_slippery':False}
)
    
env = gym.make('FrozenLake-v3', render_mode='ansi')

# Q 테이블 생성
Q = np.zeros([env.observation_space.n, env.action_space.n])
dis = 0.99 # discount factor
num_episodes = 2000
# episode마다의 총 리워드
rList = []

for i in range(num_episodes):
    state = env.reset()[0]
    rAll = 0 # 리워드 총합
    done = False
    e = 0.1 / (i+1) # e-greedy factor

    while not done:
        # e-greedy
        if np.random.rand(1) < e:
            action = env.action_space.sample()
        else:
            # Q(a,s)에 random noise 추가(decaying)
            action = np.argmax(Q[state, :] + np.random.randn(1, env.action_space.n) / (i+1))

        new_state, reward, done, truncated, info = env.step(action)

        # discount future reward(decay rate)
        Q[state, action] = reward + dis * np.max(Q[new_state, :])
        
        rAll += reward
        state = new_state

    rList.append(rAll)
    
#최종 Q 테이블 출력
print("Final Q-Table Values")
print("LEFT DOWN RIGHT UP")
print(Q)
    
#시각화
print("Success rate: " + str(sum(rList)/num_episodes))
plt.bar(range(len(rList)), rList, color="blue")
plt.show()

6-1. 실행 결과

실행 결과 0.9295로 높은 성공률을 보이며, 최종 Q 테이블은 아래와 같다. 코드에 random을 포함하고 있기에 실행 결과는 매번 달라질 수 있다.

순서대로 (LEFT,DOWN,RIGHT,UP) - 소수점 아래 2자리 수까지만 표시

\[\begin{align*} &[[0.\,0.95\,0.\,0.94][0.\,0.\,0.\,0.][0.\,0.97\,0.\,0.][0.\,0.\,0.\,0.] \\ &\;[0.\,0.96\,0.\,0.][0.\,0.\,0.\,0.][0.\,0.98\,0.\,0.][0.\,0.\,0.\,0.] \\ &\;[0.\,0.\,0.97\,0.][0.\,0.98\,0.\,0.][0.\,0.99\,0.\,0.][0.\,0.\,0.\,0.] \\ &\;[0.\,0.\,0.\,0.][0.\,0.\,0.99\,0.][0.\,0.\,1.\,0.98][0.\,0.\,0.\,0.]] \end{align*}\]

참고

Sung Kim 강사님의 모두를 위한 RL